Shaheed Anwar Girls College Admission Circular & Result 2025
Shaheed Anwar Girls College Admission Circular 2025. HSC Admission Circular 2025-2026. SAGC Nursery Admission Notice 2025. Shaheed Anwar Girls College Nursery Admission Result 2025. SAGC Nursery and Class 9 Admission Notice 2025. Shaheed Anwar School KG, Class 7, Class 8 Admission 2025. Shaheed Bir Uttam Llt Anwar Girls’ School & College Nursery Admission Notice 2024. www.sagc.edu.bd admission result. Students can apply for admission in Bangla Medium and English Version. Guardian can apply online form from October 1, 2024 to November 9, 2024. Application forms are available in room no 103 ground floor for Class II, II, IV, V, VI, VII, VIII and IX.
Admission written test will be applicable for class One to Nine. Class 1 applicant have to face viva exam before written test. Only one guardian will be allowed with applicant during viva exam. VIVA exam date & schedule will publish soon. Class six and Class 9 selected students have to submit PSC & JSC attached mark sheet during admission.
Shaheed Anwar Girls School Nursery admission schedule 2025:
Nursery Admission Application open 1/10/2024
Nursery Admission Application date close 9/11/2024
Admit Card download last date
Nursery Primary Selection viva date 1/12/2019 to 5/12/2019
Nursery (Bangla, Morning) Lottery date: December 14, 2019 at 9:00 AM
SAGC Nursery (English, Morning) Lottery date: December 14, 2019 at 11:30 AM
Nursery (Bangla, Day) Lottery date: December 14, 2019 at 2:00 PM
KG, Class 7, 8, 9 Bangla, Morning Admission test: December 12, 2016 at 9:00 AM
KG, Class 1, 3, 4, 6, 9 Day Shift, Bangla Admission test: December 10, 2016 at 9:00 AM
Applicants age 4 years to 5 years as on January 1, 2017, they can only apply for class 1. They have to submit attached birth date certificate to certify students age. Application form fee Tk. 250/ with prospectus.
Students can apply for English version for class Play, Nursery, KG, One, Two. Necessary age for different classes are given bellow: Nursery: 4 Years to 5 years. Students will get details in prospectus. www.sagc.edu.bd
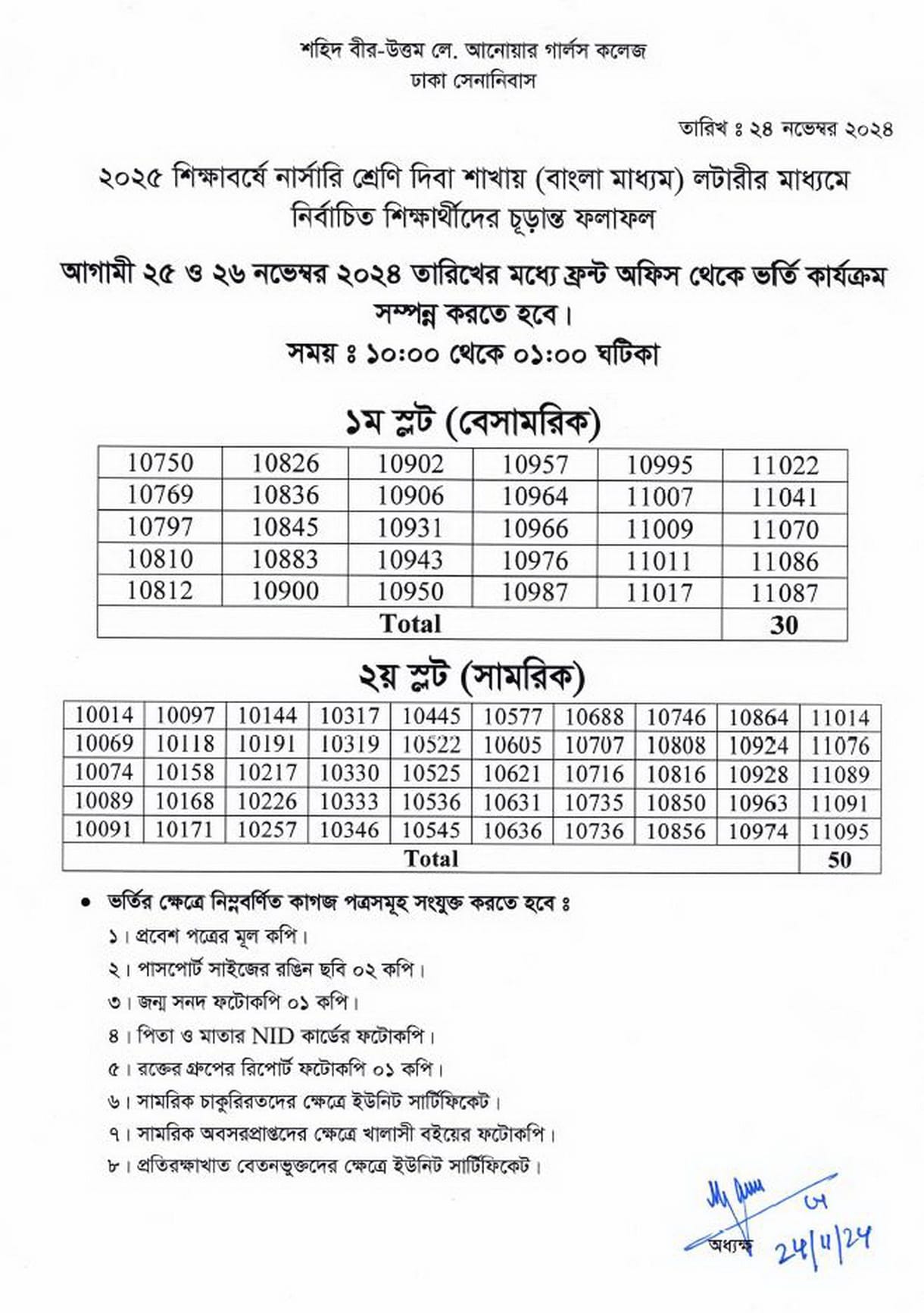
SAGC Nursery Admission Lottery Result 2025 date 24-11-2024
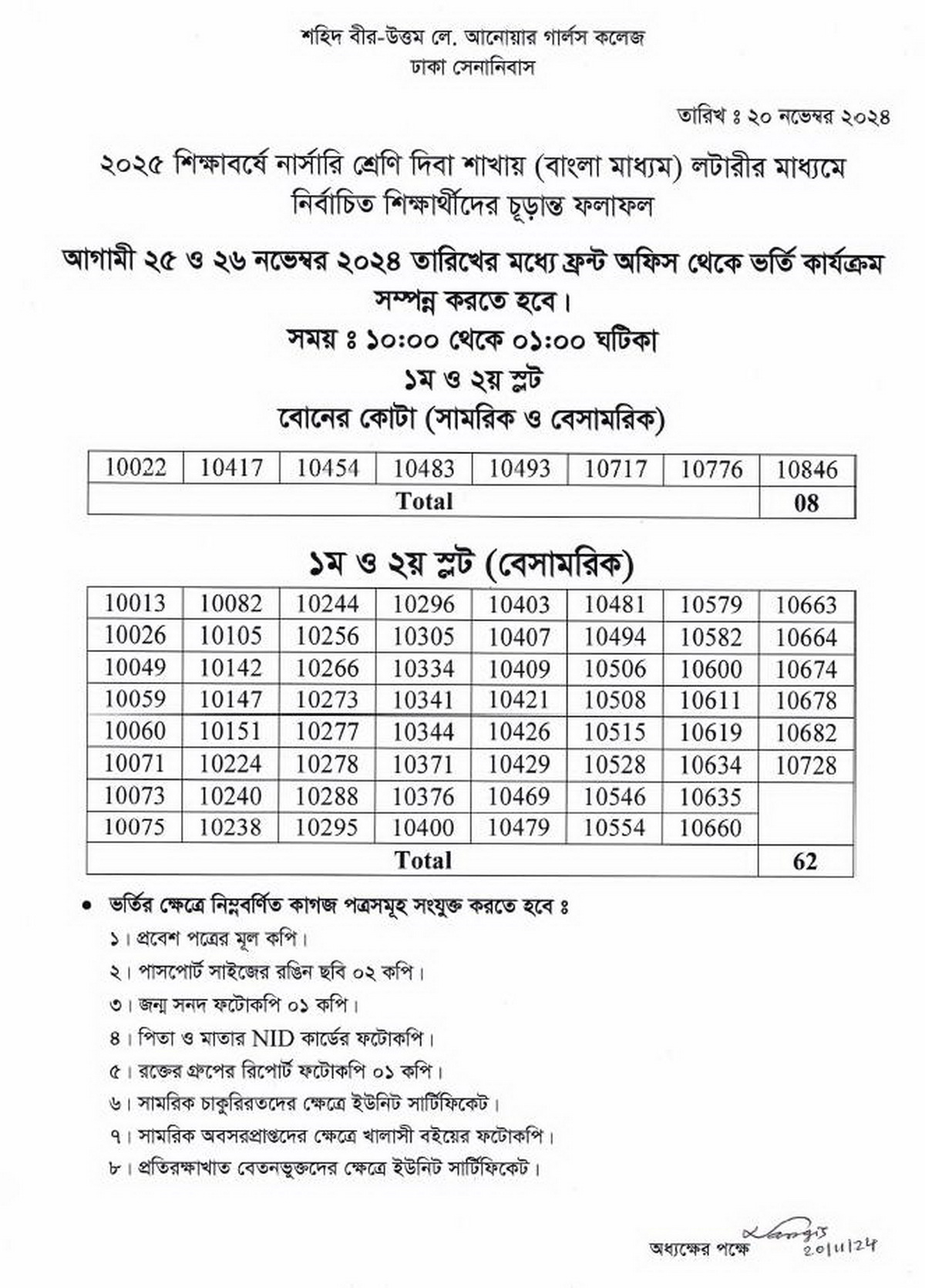
Shaheed Anwar Nursery Admission Lottery Result 2025 date 20-11-2024
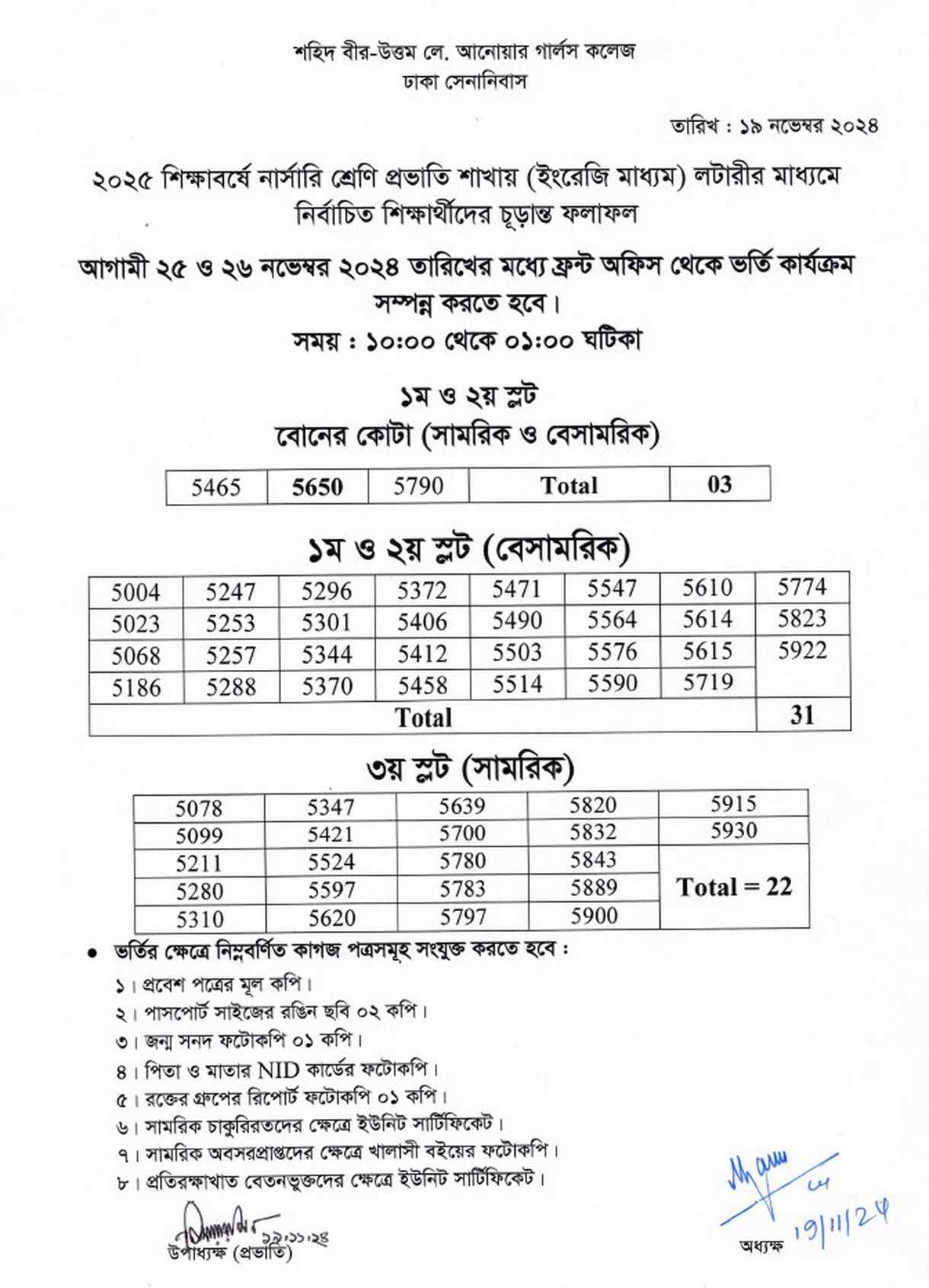
Shaheed Anwar Nursery Admission Lottery Result 2025 date 19-11-2024
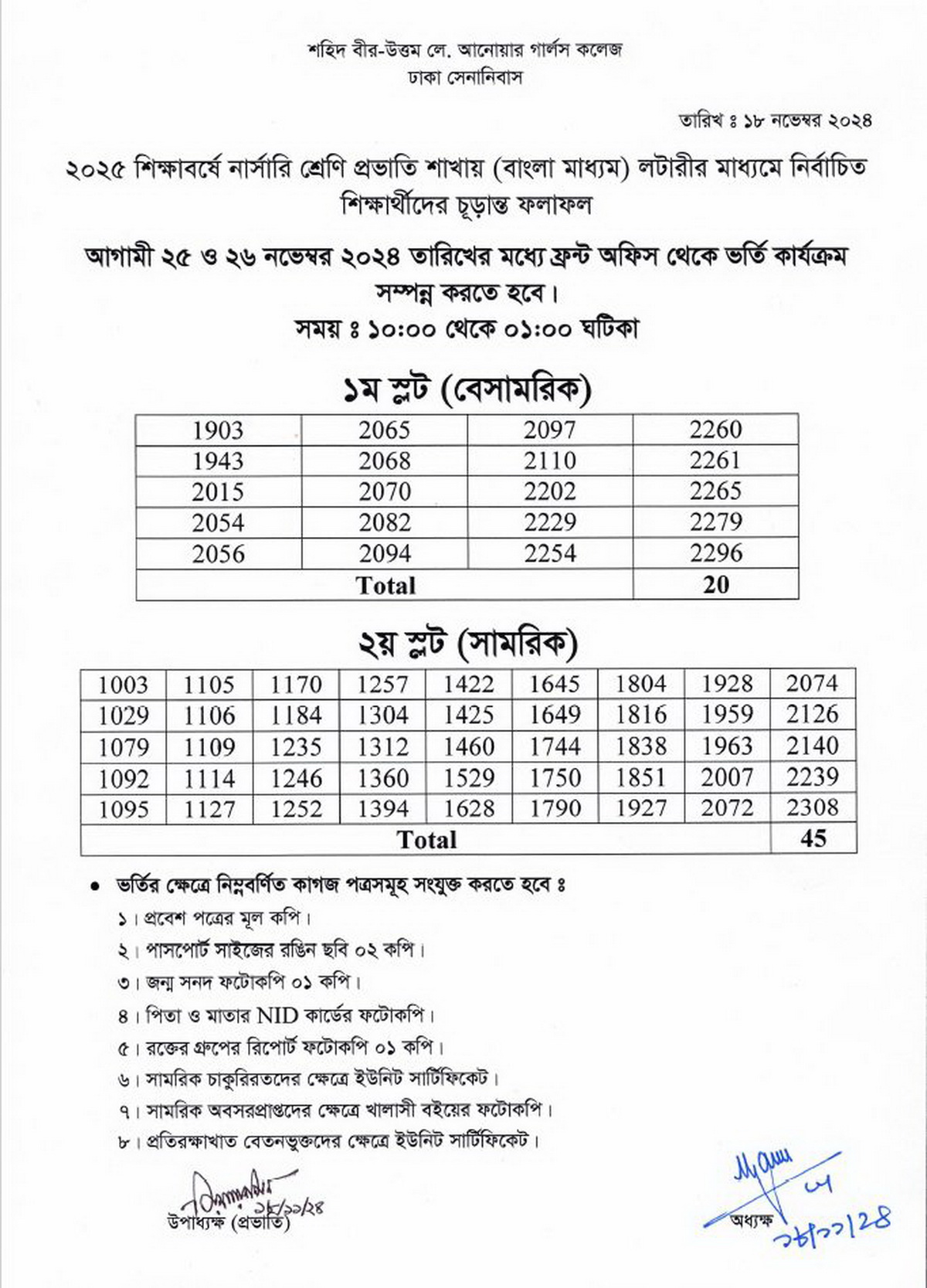
SAGC Nursery Admission Lottery Result 2025 date 18-11-2024
SAGC Nursery Admission Lottery 1st Slot Result 2025
Shaheed Anwar Girls School Nursery & Class 9 Admission Circular 2025
SAGC HSC Admission Circular 2024-25
SAGC Nursary and Class 9 Admission Circular 2024
Shaheed Anwar Girls College HSC Admission Circular 2023-24
Shaheed Anwar Girls College HSC Admission Circular 2022-23
01-12-2022 Nursery Lottery Result 2023
30-11-2022 Nursery Lottery Result 2023
29-11-2022 Nursery Lottery Result 2023
28-11-2022 Nursery Nursery Lottery Result 2023
27-11-2022 Nursery Nursery Lottery Result 2023
SAGC Nursery Nursery Admission Lottery date 2023
Shaheed Anwar Girls School Nursery & Class 9 Admission Circular 2023
Shaheed Anwar Girls College HSC Admission Circular 2021-22




Class 8 er abar 2025 er circular kobe charbe?. Exam ki hbe?
class 8 er dibe kina ekhono thik hoyni
Thanks for your reply, can you pls advise me the procedure of admission in class#VI, English version
without circular.
Sorry
Is there class 1 admission.can
no. only Nersery
when class#VI (SIX) -English version circular will be published ? if not publish, is there any other way to admit in class#VI ? Pls help to confirm.
normally circular dai na
how can i get admission to class 8 ev?
ekhono circular dai ni
How can I get admition from class 5 (Five)
circular na dile parben na
Is there any chance to admit class II in 2022 English Version?
NO
How can I get admition from class 2 or 3.
circular dile abedon korte parben
How can i apply for class 8?
circular dai ni. circular dile online a apply korte parben
class 8 English version e kibhabe admission e apply korbo?
How can I get the form for class 7 admission 2022?
How can I apply for the online application
circular dile apply korte hobe
How can i apply class 1
u can apply for nursery
only class 3, 6 and 9 admission hobe
Pls send me the admform of class six english version
u have to apply online
Circular ki ses hoyce?
3, 6 and 9 admission ki hobe, 2022 er jonno?
Govt school er shate circular chilo. Takhon jara apply koreche tara vorti hote parbe
Class 3 er ki admission hobe?
normally class 3 nai na alada vabe